1LocusSim: SIMULACIÓN DE UN LOCUS CON DERIVA GENÉTICA, MUTACIÓN Y SELECCIÓN

 

Características
  1. 1LocusSim es un simulador sencillo y adaptable (apto para móviles) para visualizar el efecto de la deriva genética, la selección y la mutación en la frecuencia alélica.
  2. Está programado en Python apoyándose en la librería NumPy.

 

Contacto
Para cualquier duda me puedes contactar .

 

Disclaimer

 

Vuelve a AC-R home
Simulación de mutación y selección
Equilibrio mutación-selección
La selección elimina alelos deletéreos pero si la mutación es recurrente estos pueden volver a aparecer antes de ser completamente eliminados de la población, de modo que se establece un equilibrio en el que la frecuencia alélica se mantiene constante. El efecto de la mutación se puede apreciar en la Figura 7 que muestra la evolución de la frecuencia de un alelo deletéreo recesivo con coeficiente de selección en contra de s=10-2. El panel A corresponde al caso sin mutación y el B al caso con mutación μ=10-3.
A     h=0, μ=0 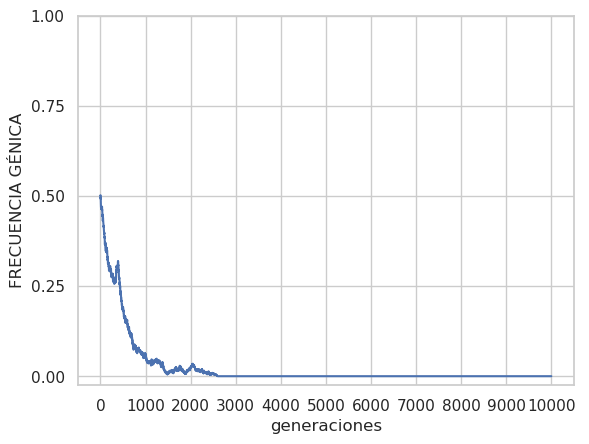Fig 7A
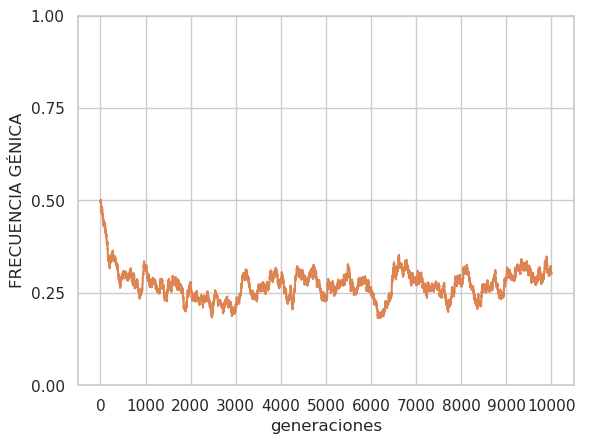
B     h=0, μ= 10-3 Fig 7B
Figura 7. Efecto de la selección sobre la frecuencia de un gen recesivo sin o con mutación. Parámetros: N=104, s=0.01, h=0.0.
En la Figura 8 se muestran las ecuaciones de equilibrio mutación selección. La retromutación se considera despreciable. La mutación genera alelos deletéreos de modo que la nueva frecuencia p' de no deletéreos corresponde a los no mutantes (1-μ). En el equilibrio, el efecto de la selección y la mutación se compensan y por tanto, Δp=0, es decir, p'=p, y obtenemos la relación entre μ y los parámetros p, q, s y h. Distinguimos entre el caso completamente recesivo (h=0) y el resto (h>0).
Figura 8. Frecuencia alélica para el equilibrio mutación-selección.
Incorporando la mutación, en ausencia de deriva (N grande) con apareamiento aleatorio y sin migración, la ecuación Δp=0, predice los valores de la frecuencia en el equilibrio. Por ejemplo, si s=0.01 y μ=s/10, si el alelo es recesivo la frecuencia de equilibrio será √0.1≈0.32, que coincide con el valor obtenido en la simulación (panel B de la Figura 7). Si el gen es aditivo, la frecuencia de equilibrio estará en torno a 0.001/(0.01×0.5) ≈ 0.2 (panel B de la Figura 9).
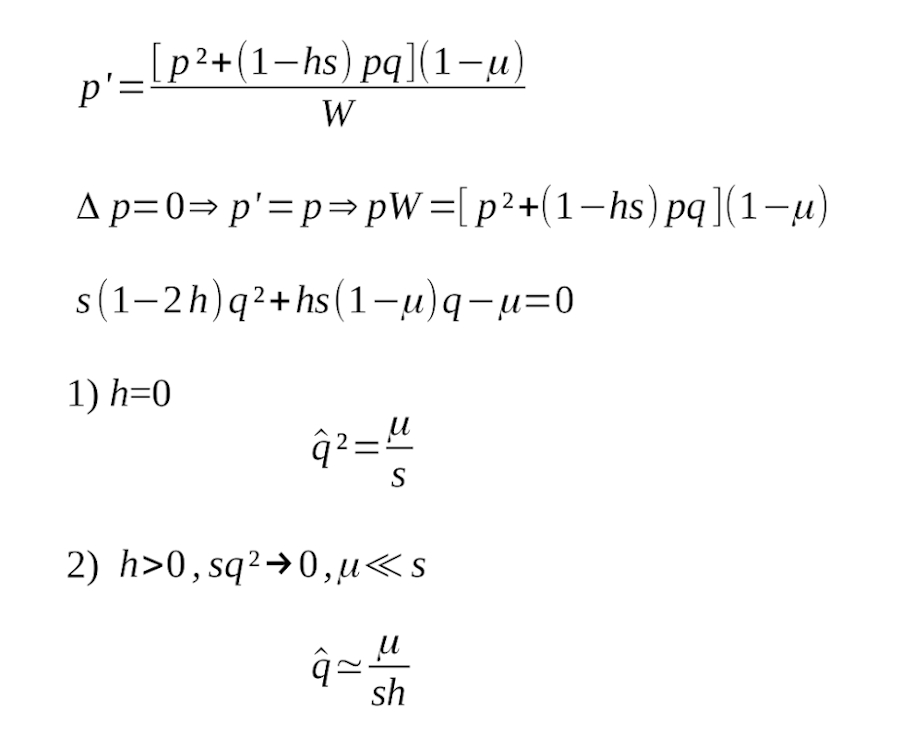
A     h = 0.5, μ=0
B     h = 0.5, μ= 10-3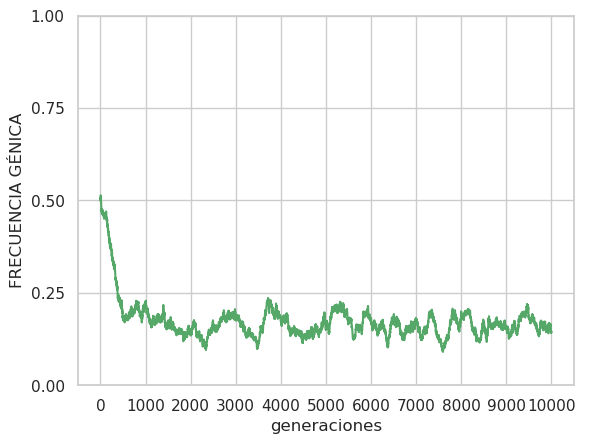
Figura 9. Efecto de la selección sobre la frecuencia alélica de un gen con aditividad, sin o con mutación. Parámetros: N=104, s=0.01, h=0.5.
Ejercicios
Utiliza las fórmulas de la Figura 8 para resolver los siguiente ejercicios.

 

Ejercicio 1
La frecuencia de un alelo deletéreo con acción génica aditiva es de 0.1 en una población en equilibrio. La tasa de mutación es 10-3 ¿Cuál es el coeficiente de selección? Si ese gen sufriera una mutación que lo convirtiera en recesivo pero manteniendo el mismo valor selectivo ¿cuál sería la nueva frecuencia de equilibrio? Si la frecuencia ha cambiado explica el porqué.

 

 Acción génica aditiva significa que h=0.5 y por tanto 0.1≈μ/(sh); solo nos resta sustituir los valores de h y la tasa de mutación y despejar para obtener s=10-3/0.05=0.02.
Si el alelo fuera recesivo qeq=(10-3/0.02)0.5=0.22. La frecuencia ha aumentado de 2% a 22% al pasar a ser recesivo porque ahora el alelo deletéreo queda oculto en los heterozigotos.

Ejercicio 2
En la misma población anterior, tenemos otro gen que es deletéreo dominante con un coeficiente de selección de 0.02. Si la tasa de mutación es 10-3 ¿Cuál es la frecuencia de equilibrio?

 

 Como el alelo deletéreo es dominante, h=1 y entonces qeq ≈10-3/0.02=0.05.

 

 

A. Carvajal-Rodriguez - Departamento de Bioquímica Genética e Inmunología - Universidad de Vigo. ( Actualizado: Marzo 2023)