1LocusSim: SIMULATION OF A LOCUS WITH GENETIC DRIFT, MUTATION AND SELECTION

 

Features
  1. 1LocusSim is a simple and adaptable (mobile-friendly) simulator to visualize the effect of genetic drift, selection and mutation on allele frequency.
  2. It is programmed in Python based on the NumPy library.

 

Contact
If you have any questions please contact me .

 

Disclaimer

 

Back to AC-R home
Simulation of mutation and selection
Mutation-selection balance
Selection eliminates deleterious alleles, but if the mutation is recurrent, they can reappear before being completely eliminated from the population, so that an equilibrium is established in which the allele frequency remains constant. The effect of the mutation can be seen in Figure 7, which shows the evolution of the frequency of a deleterious recessive allele with a selection coefficient of s=10-2. Panel A corresponds to the case without mutation and panel B to the case with mutation μ=10-3.
A     h=0, μ=0 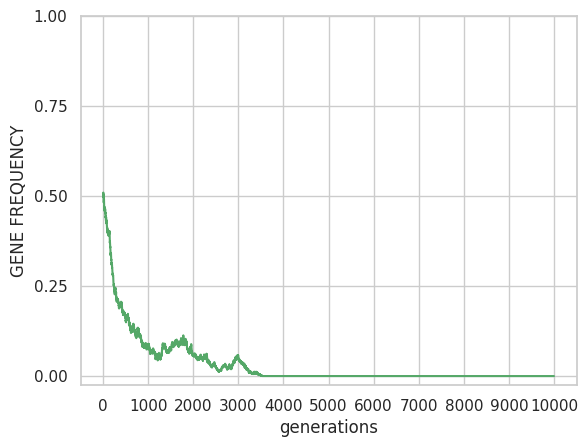Fig 7A
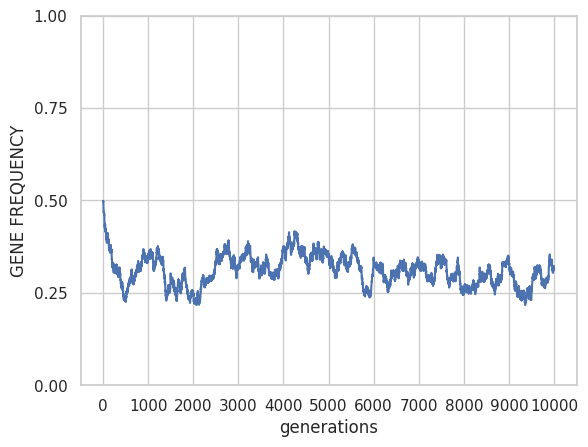
B     h=0, μ= 10-3 Fig 7B
Figure 7. Effect of selection on the frequency of a recessive gene without or with mutation. Parameters: N=104, s=0.01, h=0.0.
Figure 8 shows the mutation-selection equilibrium equations. Backmutation is considered negligible. The mutation generates deleterious alleles such that the new frequency p' of non-deleterous corresponds to the non-mutants (1-µ). At equilibrium, the effect of selection and mutation cancel each other out and therefore Δp=0, i.e. p'=p, and obtain the relation between μ and the parameters p, q, s, and h. We distinguish between the completely recessive case (h=0) and the rest (h>0).
Figure 8. Allelic frequency for mutation-selection balance.
Incorporating the mutation, in the absence of genetic drift (large N) with random mating and no migration, the equation Δp=0, predicts the equilibrium frequency values. For example, if s=0.01 and μ=s/10, if the allele is recessive the equilibrium frequency will be √0.1≈0.32, which coincides with the value obtained in the simulation (panel B of Figure 7). If the gene is additive, the equilibrium frequency will be around 0.001/(0.01×0.5) ≈ 0.2 (panel B of Figure 9).
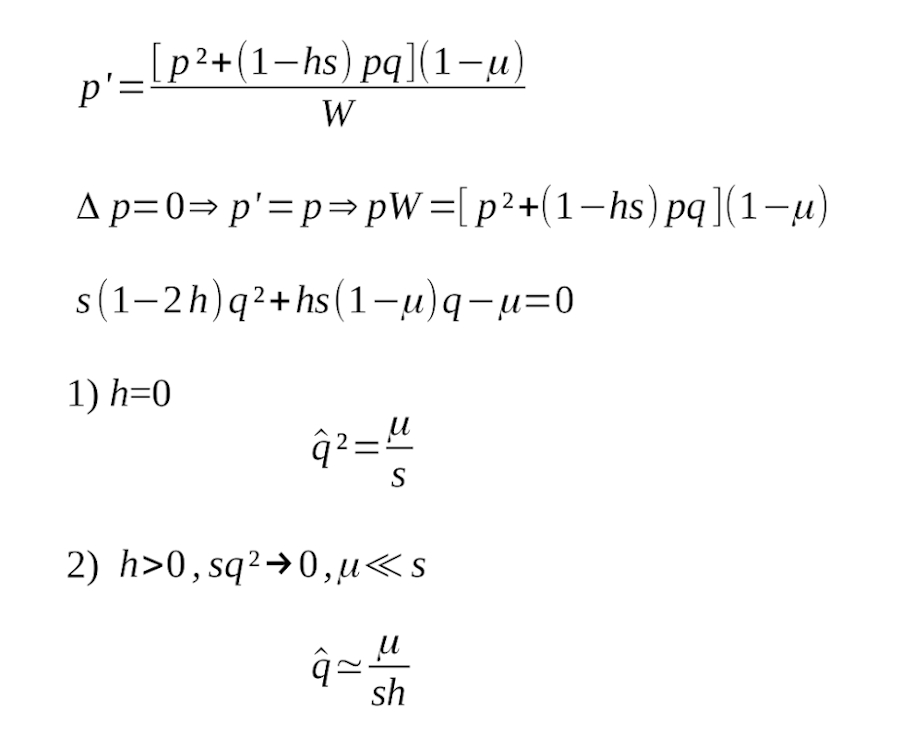
A     h = 0.5, μ=0
B     h = 0.5, μ= 10-3
Figure 9. Effect of selection on the allelic frequency of a gene with additivity, without or with mutation. Parameters: N=104, s=0.01, h=0.5.
Exercises
Use the formulas in Figure 8 to solve the following exercises.

 

Exercise 1
The frequency of a deleterious allele with additive gene action is 0.1 in a population at equilibrium. The mutation rate is 10-3, what is the selection coefficient? If that gene suffered a mutation that made it recessive but maintaining the same selective value, what would the new equilibrium frequency be? If the frequency has changed, explain why.

 

 Additive gene action means that h=0.5 and therefore 0.1≈μ/(sh). We just have to plug in the values of h and the mutation rate and solve to get s=10-3/0.05=0.02.
If the allele were recessive qeq=(10-3/0.02)0.5=0.22. The frequency has increased from 2% to 22% by becoming recessive because the deleterious allele is now hidden in heterozygotes.

Exercise 2
In the same population above, we have another gene that is deleterious dominant with a selection coefficient of 0.02. If the mutation rate is 10-3, what is the equilibrium frequency?

 

 Since the deleterious allele is dominant, h=1 and therefore qeq≈10-3/0.02=0.05.

 

 

A. Carvajal-Rodriguez - Departamento de Bioquímica Genética e Inmunología - Universidad de Vigo. ( Updated: April 2023)